
Quantum computers have the potential to fundamentally change digital technology and therefore the ways in which we solve problems, interact and do business. In her series for Roman Road Journal, science writer Gemma Milne looks into how quantum computers work and how they might change our lives. In Part 2, she explores how we use encryption to keep our data safe, and how quantum computing could be a complete game-changer.
Secret messages are an important part of our society. There’s hiding your identity so you can send emails to journalists, blowing the whistle on corporate wrongdoing, or simply buying a new toaster online without anyone stealing your credit card details in the process. It all requires encryption to ensure your information is kept firmly behind lock and key.
Encryption works very well, as at the root of it is a hard problem which no human or computer can currently solve in a quick enough time. It relies on the difficulty of a what’s called ‘prime factorisation’ – a problem so hard that it takes conventional computers hundreds of years to get to the solution. You can actually win one million dollars from the Millenium Prize Fund if you find a shortcut to get you, or a computer, to the answer quickly.
Quantum computers are a different kind of computer – and, once we manage to create a fully working one, they will be able to solve these specific, very difficult kinds of mathematical problems. Problems which conventional computers either cannot solve at all, or ones which would take them so long to get to the solution that there’s really not much point even trying.
Prime factorisation – and, thus cracking encryption – is one such problem which, for a working quantum computer of the future, would be easy. And this, of course, brings problems of its own.

A representation of quantum particles in action
A Prime Problem
Any number can be broken down into its prime factors. A number’s factors are the ones that multiply together to result in your original number. So for instance, if you wanted to find the factors of 20, you would find that they are 1, 2, 4, 5, 10, and 20 – because all of these numbers can be used in some form of multiplication to get the answer 20 (1 x 20 = 20; 2 x 10 = 20; 4 x 5 = 20). Now, a prime number only divides by itself and by 1. If you were to find the prime factors of 20, you’d start dividing down using only basic prime numbers until you can divide no further. So 20 divided by 2 is 10; 10 divided by 2 is 5. 2 and 5 are both primes as you cannot divide them down any further except by using 1 or themselves – so 20 written as a product of its prime factors is 2 x 2 x 5, and 20’s prime factors are 2 and 5.
This is a super simple process when you have numbers which easily divide by small primes like 2 and 5. But if I were to give you the number 515,443, you’d soon find that it doesn’t nicely divide by 3 or 7 or 11 or any of the first 126 primes we know. In fact, the only two numbers which divide 515,443 are themselves primes – 709 and 727 – and so you’d only be able to work this out by literally going through the list of primes one by one and testing if they work.
So what does this have to do with encryption? In order to encrypt a message (turn it into a gobbledygook coded message), you need to have a process for making it a random mess so that criminals – or simply those you want to keep out – can’t understand it, as well as a process for turning it back into something legible for whoever you wish to read it. You have what’s called a ‘public key’ – a number you get from multiplying two huge prime numbers together; and a ‘secret key’ – the two primes themselves. You can make the public key public – your bank sort code and account number, for example – but only you know the secret key which is used to decrypt the secret message: ‘use this information to pay Amazon for my lovely new toaster’. If anyone wanted to try and break into that message, they’d have to sit and factor that huge number without any hints of the primes. This would take so long – hundreds of years – that by the time that person managed to get hold of your bank information, you, and they, would most likely be dead.
The fact that prime factorisation is such a hard problem is at the root of why encryption works.
Of course, we have built computers which can do the boring, time consuming task of finding simple prime factors for us, but when it comes to large numbers – ones which you get by multiplying two prime numbers with over fifty digits, for example – even our computers become sluggish and slow in going one by one through these primes to find the answer. There’s no shortcut for this – it’s literally a trial and error process – and because it’s such a long process to solve, it works perfectly as a basis for protecting our information from people trying to steal it.
But Now What?
Working quantum computers are coming, and prime factorisation is a kind of problem which can theoretically easily be solved by them. So security companies have to come up with new ways of doing encryption – fast. They are playing with complex mathematical problems to see if they can find other questions so hard to answer that even a quantum computer is no match.
Lattice Problems are types of problems regarding various different kinds of grids and the routes between the points within them. For example, say you had the grid below and you wanted to find the shortest path between any 2 points (shown here by the one in red), this would not be possible using a conventional or quantum computer, for every kind of grid. Looks easy, yes, but the lines of code and mathematics is frightening even for the most adept number crunchers.
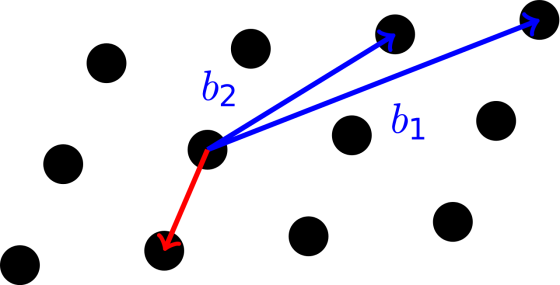
There are a few different kinds of ‘quantum-safe’ problems which could replace prime factorisation, but until a quantum computer is at the point of being useful and can be used to test such ideas, we’re still working in theoretical realms.
Technology’s Downside
Quantum computers are going to change our world – disrupting the slow process of drug discovery and helping us create new, more sustainable, ways of manufacturing our planet. But no new technology comes without challenges.
It may sound simply like big companies having to shell out money to update their systems, but when you consider the scale of the encryption world, much is at stake. Governments, media organisations, messaging apps, banks – all places where the regular person counts on security – would have to ensure they are set up for a quantum world. The time, energy and money needed to make these changes could be crippling, especially for those late to the party.
But the benefits of quantum computing do seem to outweigh the challenges, and with more and more research and corporate effort being dedicated to bringing them into the real world, quantum-safe cryptography needs to stay well ahead.
That is, of course, assuming that the money funding the hugely expensive task of developing these machines doesn’t dry up before they come into existence…
To be continued in Part 3
Read Part 1 here
—
Gemma Milne is a Science & Tech writer, and is Co-Founder of media startup Science: Disrupt. You can find her on Twitter @gemmamilne or at her website www.gemmamilne.co.uk